
>>>点击查看ACT考试完整盘点<<<
新东方网留学频道特邀新东方北美考试部VIP项目的周柏为老师为大家带来ACT数学函数的渐近线,希望对大家2016年的ACT备考有所帮助。
大家好,我是新东方北美VIP部的数学老师周柏为,今天我给大家带来的是ACT数学中函数渐近线的求法。很多同学没有学过微积分,并不知道这种问题怎么去解决,可以看作是ACT数学考试中的一个难点,所以今天我们有必要在这里重点讲一下。
函数的极限问题
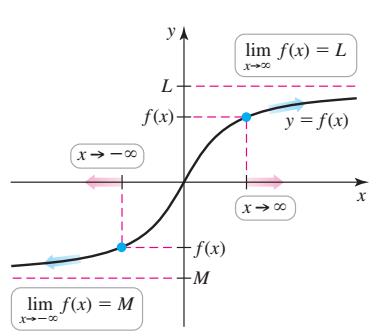
在讲函数渐近线之前,我们首先来了解一下函数的极限问题。极限在微积分中的定义非常复杂,可以简单去理解。我们来看下方这个图象,当x趋近于无穷的时候,即无限大的时候,y的值无限趋近于M,所以我们就把M当作x趋近无穷时y的极限。而当x无限趋近a的时候,函数y的值趋近于无穷,所以我们就把y等于无穷作为x趋近于a的一个极限。而当x趋近于负无穷的时候呢, y趋近于L,所以L就是x趋近于负无穷时y的极限。
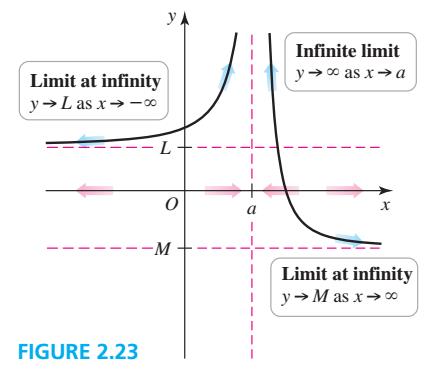
渐近线所用的正是极限的原理,x趋近于无穷的时候,y趋近于M, y=M是这条水平的直线,函数图象无限趋近于这条直线,所以这条线就成为了一条函数的渐近线。通过这个图象,我们可以看到它有两条水平的渐近线:y=M和y=L。然后还有一条竖直的渐近线是x=a这条直线。
竖直渐近线的求法
在ACT数学考试中,竖直渐近线和水平渐近线是一个重点,频繁出现,我们首先来看一下竖直渐近线应该怎么来求。
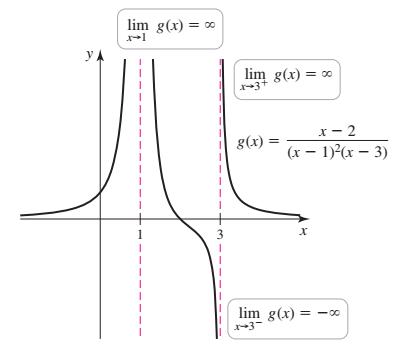
上图显示的这个函数,分子是(x-2),分母是(x-1)的平方和(x-3)。
这个图象画出来可以很清晰地看到它的竖直渐近线是x=1和x=3,但具体应该怎么求呢?我们可以看到当x趋近于3的时候,无论从左边还是右边趋近的时候,这个y都是趋近于无穷的,所以x=3就变成了它的一条竖直渐近线;而x趋近于1的时候也是一样的,无论左边还是右边趋近,y都是趋近于正无穷的,所以x=1就变成它的一条竖直渐近线。
下面我们看一下竖直渐近线的定义,当x无限趋近于k的时候(k负就是从左边无限靠近k,k正就是从右边无限靠近k),这个y的值,也就是f(x)的值是趋近于正负无穷的,那么我们就把x=k记做这个函数的竖直渐近线。
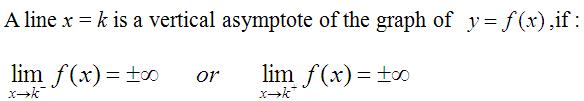
我们来看下面这个例子,limit就是极限的意思,当x无限趋近于3负,即从左边无限靠近3的时候,分子是(2-5x)此时趋近于-13。计算方法是把3带入,而分母是(x-3)在x趋近于3的时候趋近于0。当分母是0分子是一个数的时候,即-13除以0的时候,这个值是没有意义的,也就是无穷。所以x=3是它的一条竖直渐近线。

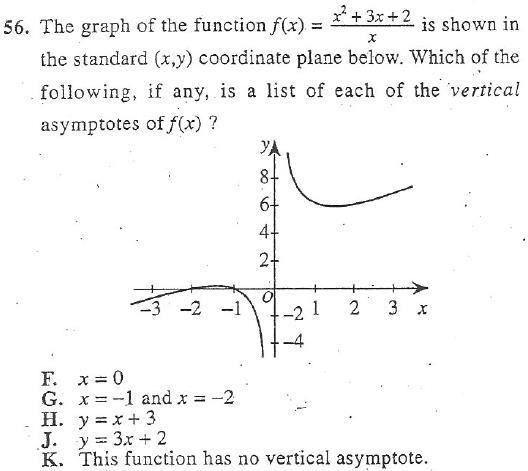
下面我们来看一下ACT考试中出现的一些问题。第一个题给出的函数分子是(201x+202),分母是(203x+204),用刚才讲的方法应该让分母趋近于0,即203x+204=0,此时分母是0的时候,分子是一个数,就会出现竖直渐近线的情况。所以得出结果x=-203/204。
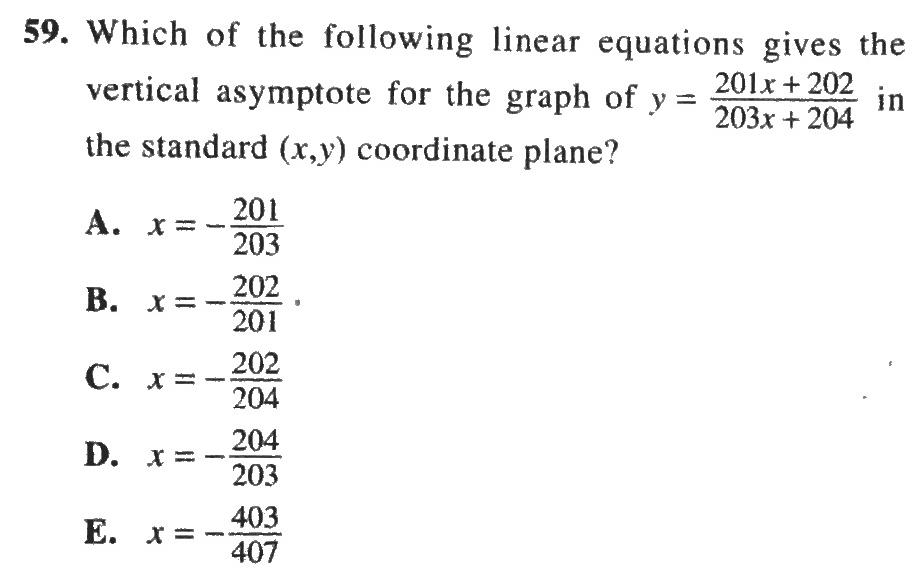
再来看第二个题。这个题比上一题简单一些,因为它已经把图象给你了。通过看图,我们看到y轴就是它的一条竖直渐近线,而看函数方程,它的分母是x,所以当x趋于0的时候,分子等2,所以x=0就是它的一条竖直渐近线。所以这道题选F。
水平渐近线的求法
竖直渐近线讲完了,再来看一下水平渐近线的求法。首先看一下这个图象,x趋近于正无穷时,函数图象无限靠近水平直线y=L;x趋近于负无穷是,函数图像无限靠近水平直线y=M。水平渐近线的定义就是,当x趋近于正无穷或者负无穷时,y趋近于的值就是它的水平渐近线。
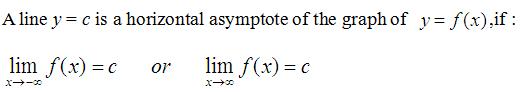
我们来看它具体的求法。一个函数分子是(40x^4+4x^2-1),而分母是(10x^4+8x^2+1),我们求的时候可以分子分母同时除以x的4次方,也就是最高次项。注意分子分母最高次项是x的4次方。除完并且约分以后,分子变成(40+4/x^2-1/x^4),而分母变成10+8/x^2+1/x^4。

因为x是趋近于无穷的,x的平方以及x的4次方也是趋近于无穷的,所以4除以一个无穷,它的值得应该是趋近于零。同理,分子分母各有两项都变成无限趋近于0,所以只剩下了40除以10,所以结果是4。
所以如果给我们一个函数是这样的形式,它的极限就应该是看最高次项的系数之比,这道题里也就是4次方的系数比,直接40除以10等于4就可以了。
来看一下ACT考试实际出现的问题。来看这个方程,它的分子是(2x^2-18),分母是(x^2-5x)。按照刚才的规律,分子分母同时除以x的平方,这样分母各有一项趋近于0,所以这个函数的这个水平线渐线就应该是y=2。

再来看第二个题,这个题看着比上一个题复杂一些,其实方法都是一样的。我们把剩下除了x的4次方以外所有的项都忽略掉,通过极限思想来考虑,就是x特别特别大的时候,这个x的4次方就是x的3次方的无限大倍,相比之下x的平方就更小了,1就更可以忽略了,所以我们只要看分子分母的最高次项就可以了。所以应该是3倍x的4次方除以2倍x的4次方,约分以后就是3/2,答案就是1.5。

那么,函数渐近线的问题我们今天就讲到这里,如果想了解更多的知识我们可以关注一下北京新东方学校北美高端考试业务。谢谢大家。

教师介绍:周柏为,出生于北国春城,曾以全校第一的成绩考入全国总排名第四的高中(东北师大附中)最强的理科实验班,大学毕业于北京邮电大学,毕业后在科研单位从事了两年的研发工作,洞悉数学应用。了解并善于疏导学生心态,亦师亦友,以幽默风趣的教风让学生在愉悦和亲切中,享受学习,享受进步。具有极强的理性思维,注重因材施教,为每个学生找到适合自己最佳的学习方法,善于剥离问题表象,发掘问题本质,通过综合分析,快速寻求问题解决方案。
高分严打造——北京新东方留学考试
走读班/住宿班报名电话:010-82611818 400-817-1818
请扫描下方二维码得价值1000元优惠

相关推荐:
2015新东方留学考试全民测之SAT-ACTStartUp测试
版权声明:本文系新东方网独家稿件,版权为新东方网所有。转载须注明来源及作者,否则必将追究法律责任。



